Operații pe biți
Operațiile pe biți se efectuează asupra bitilor individuali ai numerelor. Aceste operații se aplică doar asupra numerelor întregi. Dar, mai întâi, să vedem pe scurt ce înseamnă pozițiile (biții) unui număr.
Reprezentarea binară a numerelor
La nivelul calculatorului, toate datele sunt reprezentate ca un set de biți. Fiecare bit poate avea două valori: 1 (semnal prezent) și 0 (fără semnal). Toate datele sunt, în esență, doar șiruri de 0 și 1. 8 biți reprezintă 1 byte. Acest sistem se numește sistem binar.
De exemplu, numărul 13 în sistem binar este 1101₂. Cum ajungem la el:
// conversia numărului zecimal 13 în sistem binar
13 / 2 = 6 // rest 1 (13 - 6 * 2 = 1)
6 / 2 = 3 // rest 0 (6 - 3 * 2 = 0)
3 / 2 = 1 // rest 1 (3 - 1 * 2 = 1)
1 / 2 = 0 // rest 1 (1 - 0 * 2 = 1)Algoritmul general constă în împărțirea succesivă a numărului și a rezultatelor obținute la 2, reținând resturile până ajungem la 0.
Apoi scriem resturile în ordine inversă și astfel obținem reprezentarea binară a numărului. În acest caz, pas cu pas:
- Împărțim numărul 13 la 2. Rezultatul împărțirii – 6, restul împărțirii – 1 (deoarece 13 - 6 * 2 = 1)
- Apoi împărțim rezultatul operației anterioare – numărul 6 la 2. Rezultatul împărțirii – 3, restul împărțirii – 0
- Împărțim rezultatul operației anterioare – numărul 3 la 2. Rezultatul împărțirii – 1, restul împărțirii – 1
- Împărțim rezultatul operației anterioare – numărul 1 la 2. Rezultatul împărțirii – 0, restul împărțirii – 1
- Ultimul rezultat al împărțirii este 0, deci încheiem procesul și așezăm resturile obținute de la operațiile de împărțire începând cu ultimul – 1101
La conversia inversă din sistemul binar în sistemul zecimal, înmulțim valoarea fiecărui bit (1 sau 0) cu 2 la puterea corespunzătoare poziției bitului (numerotarea bitilor începe de la zero):
// conversia numărului binar 1101 în sistem zecimal
1 (bitul 3) 1 (bitul 2) 0 (bitul 1) 1 (bitul 0)
1 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2⁰
=
1 * 8 + 1 * 4 + 0 * 2 + 1 * 1
=
8 + 4 + 0 + 1
=
13Reprezentarea numerelor negative
Pentru reprezentarea numerelor cu semn în C++ se folosește complementul față de doi (two's complement), unde bitul cel mai semnificativ (cel mai din stânga) este bitul de semn. Dacă valoarea acestuia este 0, atunci numărul este pozitiv, iar reprezentarea binară nu diferă de cea a unui număr fără semn.
De exemplu, 0000 0001 în sistem zecimal este 1. Dacă bitul cel mai semnificativ este 1, atunci avem de-a face cu un număr negativ. De exemplu, 1111 1111 în sistem zecimal reprezintă -1. În mod similar, 1111 0011 reprezintă -13.
Pentru a obține un număr negativ dintr-un număr pozitiv, se aplică următorii pași:
- Inversăm toți biții (1 devine 0 și 0 devine 1)
- Adăugăm 1 la rezultat
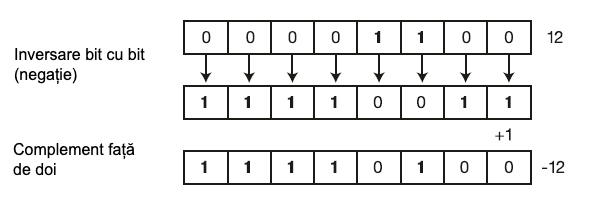
De exemplu, să obținem numărul -3. Pentru aceasta, mai întâi luăm reprezentarea binară a numărului 3:
3₁₀ = 0000 0011₂
Inversăm biții:
~0000 0011 = 1111 1100
Și adăugăm 1:
1111 1100 + 1 = 1111 1101
Astfel, numărul 1111 1101 reprezintă în binar valoarea -3.
Să analizăm cum are loc adunarea unui număr cu semn și a unuia fără semn. De exemplu, să adunăm 12 și -8:
12₁₀ = 00001100₂
+
-8₁₀ = 11111000₂ (8 = 00001000, după inversare: 11110111, +1 = 11111000)
=
4₁₀ = 00000100₂
Vedem că în sistem binar am obținut numărul 00000100₂, adică 4 în sistem zecimal.
Pentru o mai bună claritate, în C++ este convenabil să folosim scrierea binară a numerelor, care este precedată de prefixul 0b:
#include <iostream>
int main()
{
unsigned int number{0b0000'1100}; // 12
std::cout << number << std::endl;
}În acest caz, variabila number are valoarea 0b0000'1100, ceea ce corespunde numărului 12 în sistemul zecimal.
Operații de deplasare (shift)
Fiecare număr întreg este reprezentat în memorie sub forma unui anumit număr de biți. Iar operațiile de deplasare permit mutarea reprezentării binare a unui număr cu un anumit număr de poziții spre dreapta sau spre stânga. Operațiile de deplasare se aplică doar operanzilor întregi. Există două tipuri de operații:
- << (Deplasează reprezentarea binară a numărului (primul operand) spre stânga cu un număr de poziții specificat de al doilea operand)
- >> (Deplasează reprezentarea binară a numărului spre dreapta cu un număr de poziții specificat)
Aplicarea operațiilor:
unsigned int a = 2 << 2; // 10 (în binar) deplasat cu două poziții la stânga = 1000 → 8
unsigned int b = 16 >> 3; // 10000 (în binar) deplasat cu trei poziții la dreapta = 10 → 2
Numărul 2 în reprezentare binară este 10. Dacă deplasăm acest număr cu două poziții spre stânga, obținem 1000, ceea ce în sistem zecimal este 8.
Numărul 16 în reprezentare binară este 10000. Dacă deplasăm acest număr cu trei poziții spre dreapta (ultimele trei biți sunt eliminați), obținem 10, ceea ce în sistem zecimal este 2.
Se poate observa că deplasarea cu un bit la stânga este echivalentă cu înmulțirea cu 2, iar deplasarea cu un bit la dreapta este echivalentă cu împărțirea la 2.
Putem generaliza:
- deplasarea la stânga cu n poziții este echivalentă cu înmulțirea numărului cu 2ⁿ,
- iar deplasarea la dreapta cu n poziții este echivalentă cu împărțirea la 2ⁿ.
Aceasta se poate folosi în locul operațiilor de înmulțire/împărțire cu puteri ale lui 2:
#include <iostream>
int main()
{
unsigned int x{3};
unsigned int number{7};
unsigned int result{number << x}; // 7 * 2*2*2 = 56
std::cout << "Result: " << result << std::endl;
number = 26;
result = number >> x; // 26 / (2*2*2) = 3
std::cout << "Result: " << result << std::endl;
}Operații pe biți
Operațiile pe biți se efectuează doar asupra pozițiilor corespunzătoare (biților) ale operanzilor întregi:
- &: conjuncție pe biți (operația ȘI sau înmulțire pe biți). Returnează 1 doar dacă ambii biți corespunzători ai celor două numere sunt 1
- |: disjuncție pe biți (operația SAU sau adunare pe biți). Returnează 1 dacă cel puțin unul dintre biții corespunzători este 1
- ^: SAU exclusiv pe biți. Returnează 1 dacă exact unul dintre biții corespunzători este 1
- ~: negație pe biți sau inversiune. Inversează toți biții operandului. Dacă un bit este 1, devine 0, iar dacă este 0, devine 1
Aplicarea operațiilor:
int a = 5 | 2; // 101 | 010 = 111 - 7
int b = 6 & 2; // 110 & 010 = 10 - 2
int c = 5 ^ 2; // 101 ^ 010 = 111 - 7
int d = ~9; // -10De exemplu, expresia 5 | 2 este egală cu 7. Numărul 5 în scriere binară este 101, iar numărul 2 este 10 sau 010. Adunăm biții corespunzători ai ambelor numere. La adunare, dacă cel puțin unul dintre biți este 1, suma este 1. Așadar, obținem:
1 0 1
0 1 0
1 1 1Rezultatul este 111, adică 7 în sistem zecimal.
Să luăm o altă expresie: 6 & 2. Numărul 6 în binar este 110, iar 2 este 010. Înmulțim biții corespunzători ai ambelor numere. Produsul este 1 doar dacă ambii biți sunt 1. Altfel, este 0. Obținem:
1 1 0
0 1 0
0 1 0Rezultatul este 010, ceea ce în sistem zecimal este 2.
Exemplu de utilizare practică a operațiilor pe biți
Mulți subestimează operațiile pe biți, neînțelegând la ce pot fi utile. Totuși, ele pot ajuta la rezolvarea multor tipuri de probleme. În primul rând, ele ne permit să manipulăm datele la nivel de biți individuali. Un exemplu: avem trei numere, fiecare aflat în intervalul de la 1 la 3:
int value1 {3}; // 0b0000'0011
int value2 {2}; // 0b0000'0010
int value3 {1}; // 0b0000'0001Știm că valorile acestor numere nu vor fi mai mari decât 3, și dorim să comprimăm aceste date cât mai eficient. Putem salva cele trei numere într-un singur număr. Iar în acest caz, operațiile pe biți ne vor fi de ajutor.
#include <iostream>
int main()
{
int value1 {3}; // 0b0000'0011
int value2 {2}; // 0b0000'0010
int value3 {1}; // 0b0000'0001
int result {0b0000'0000};
// salvăm în result valoarea din value1
result = result | value1; // 0b0000'0011
// deplasăm biții din result cu 2 poziții la stânga
result = result << 2; // 0b0000'1100
// salvăm în result valoarea din value2
result = result | value2; // 0b0000'1110
// deplasăm biții din result cu 2 poziții la stânga
result = result << 2; // 0b0011'1000
// salvăm în result valoarea din value3
result = result | value3; // 0b0011'1001
std::cout << result << std::endl; // 57
}Să analizăm acest cod. Mai întâi, sunt definite toate valorile care trebuie stocate: value1, value2, value3. Pentru stocarea rezultatului este definită variabila result, care inițial este egală cu 0. Pentru o mai bună claritate, i-a fost atribuită o valoare în format binar:
int result = 0b0000'0000;Salvăm primul număr în result:
result = result | value1; // 0b0000'0011Aici avem de-a face cu o operație logică de adunare pe biți – dacă unul dintre biții corespunzători este 1, atunci bitul rezultat va fi și el 1. Cu alte cuvinte, practic:
0b0000'0000
+
0b0000'0011
=
0b0000'0011Așadar, primul număr a fost salvat în result. Vom salva numerele în ordine. Adică, mai întâi în result va fi primul număr, apoi al doilea și apoi al treilea. De aceea, deplasăm result cu două poziții la stânga (deoarece fiecare număr ocupă în memorie cel mult doi biți).
result = result << 2; // 0b0000'1100Adică, practic efectuăm următorul calcul:
0b0000'0011 << 2 = 0b0000'1100Apoi repetăm operația logică de adunare, salvăm al doilea număr:
result = result | value2; // 0b0000'1110ceea ce este echivalent cu:
0b0000'1100
+
0b0000'0010
=
0b0000'1110Apoi repetăm deplasarea cu două poziții spre stânga și salvăm al treilea număr. În cele din urmă, vom obține în reprezentare binară numărul 0b0011'1001. În sistemul zecimal, acest număr este egal cu 57. Dar acest lucru nu are importanță, deoarece ne interesează biții specifici ai numărului. Merită menționat că am salvat trei numere într-un singur număr, iar în variabila result mai există spațiu liber. De altfel, în realitate nu contează câți biți trebuie salvați exact. În acest exemplu, salvăm doar doi biți.
Pentru a restabili datele, vom recurge la ordinea inversă:
#include <iostream>
int main()
{
int result {0b0011'1001}; // Valoarea inițială care conține cele 3 numere ambalate (împachetate) în binar
// recuperăm ultimii 2 biți (valoarea 3)
int newValue3 = result & 0b000'0011;
// deplasăm spre dreapta cu 2 biți pentru a extrage următoarea valoare
result = result >> 2;
int newValue2 = result & 0b000'0011;
// din nou, deplasăm spre dreapta cu 2 biți
result = result >> 2;
int newValue1 = result & 0b000'0011;
// Afișăm valorile extrase în ordinea în care au fost împachetate inițial
std::cout << newValue1 << std::endl; // 3
std::cout << newValue2 << std::endl; // 2
std::cout << newValue3 << std::endl; // 1
}Obținem numerele în ordine inversă față de cea în care au fost salvate. Deoarece știm că fiecare număr salvat ocupă doar doi biți, practic trebuie să extragem doar ultimii doi biți. Pentru aceasta, aplicăm o mască de biți 0b000'0011 și o operație de „înmulțire logică” (AND logic), care returnează 1 doar dacă ambii biți corespunzători sunt egali cu 1. Adică, operația:
int newValue3 = result & 0b000'0011;este echivalentă cu:
0b0011'1001
*
0b0000'0011
=
0b0000'0001Astfel, ultimul număr este egal cu 0b0000'0001, adică 1 în sistem zecimal.
Merită menționat că, dacă știm cu exactitate structura datelor, atunci putem construi cu ușurință o mască de biți pentru a obține numărul dorit:
#include <iostream>
int main()
{
int result {0b0011'1001};
int recreatedValue1 = (result & 0b0011'0000) >> 4;
std::cout << recreatedValue1 << std::endl;
}Aici obținem primul număr, despre care știm că ocupă al treilea și al patrulea bit din numărul compus. Pentru aceasta, aplicăm o mască de biți 0b0011'0000. Apoi deplasăm numărul cu 4 poziții spre dreapta.
0b0011'1001
*
0b0011'0000
=
0b0011'0000
>> 4
=
0b0000'0011În mod similar, dacă știm cu exactitate structura după care sunt salvate datele, atunci am putea salva direct datele în poziția dorită din numărul result:
#include <iostream>
int main()
{
int value1 {3}; // 0b0000'0011
int value2 {2}; // 0b0000'0010
int value3 {1}; // 0b0000'0001
int result {0b0000'0000}; // inițializăm rezultatul cu 0
// salvăm value1 în biții 4 și 5
result = result | (value1 << 4);
// salvăm value2 în biții 2 și 3
result = result | (value2 << 2);
// salvăm value3 în biții 0 și 1
result = result | value3;
// rezultat final: 0b0011'1001 => 57 în zecimal
std::cout << result << std::endl; // 57
}