Operațiile pe biți

Operațiile pe biți sunt efectuate asupra fiecărui bit sau cifră individuală a numerelor. Aceste operații se aplică numai asupra numerelor întregi. Mai întâi să analizăm pe scurt ce reprezintă cifrele numerelor.

Reprezentarea binară a numerelor

La nivelul computerului, toate datele sunt reprezentate în formă de set de biți. Fiecare bit poate avea două valori: 1 (există semnal) și 0 (nu există semnal). Și toate datele sunt efectiv reprezentate ca un set de zerouri și unu. 8 biți reprezintă 1 byte. Această sistemă este numită binară.

De exemplu, numărul 13 în sistemul binar va fi 1101. Cum am obținut acest rezultat:

Conversia numărului zecimal 13 în sistem binar arată astfel:

13 / 2 = 6 // rest 1 (13 - 6 * 2 = 1) 6 / 2 = 3 // rest 0 (6 - 3 * 2 = 0) 3 / 2 = 1 // rest 1 (3 - 1 * 2 = 1) 1 / 2 = 0 // rest 1 (1 - 0 * 2 = 1)

Algoritmul general constă în împărțirea secvențială a numărului și a rezultatelor împărțirii la 2, obținerea resturilor, până când se ajunge la 0. Apoi, resturile sunt aliniate în ordine inversă, formând astfel reprezentarea binară a numărului. În acest caz specific, pașii sunt următorii:

• Împărțim numărul 13 la 2. Rezultatul împărțirii este 6, iar restul este 1 (deoarece (13 - 6 * 2 = 1).
• Apoi împărțim rezultatul operației anterioare, adică numărul 6, la 2. Rezultatul împărțirii este 3, iar restul este 0.
• Împărțim rezultatul operației anterioare, adică numărul 3, la 2. Rezultatul împărțirii este 1, iar restul este 1.
• Împărțim rezultatul operației anterioare, adică numărul 1, la 2. Rezultatul împărțirii este 0, iar restul este 1.

Ultimul rezultat al împărțirii este 0, deci procesul este încheiat, iar resturile operațiilor de împărțire sunt aliniate, începând cu cel din urmă - 1101.

La conversia inversă din sistemul binar în cel zecimal, înmulțim valoarea fiecărui bit (1 sau 0) cu 2 la puterea corespunzătoare numărului bitului (numerotarea începe de la zero):

// traducerea numărului binar 1101 în sistemul zecimal 1 (bitul 3) 1 (bitul 2) 0 (bitul 1) 1 (bitul 0) 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 1 * 8 + 1 * 4 + 0 * 2 + 1 * 1 = 8 + 4 + 0 + 1 = 13

În JavaScript, pentru a defini numere în format binar, se aplică prefixul 0b:

const număr = 0b1101;  // 13 în sistemul zecimal
console.log(număr);   // 13

Reprezentarea Numerelor Negative

În JavaScript, se folosește complementul a doi pentru a reprezenta numerele semnate, unde cel mai semnificativ bit servește ca indicator de semn. Dacă valoarea sa este 0, atunci numărul este pozitiv, iar reprezentarea sa binară este identică cu cea a unui număr fără semn. De exemplu, 0000 0001 în sistemul zecimal este 1.

Dacă cel mai semnificativ bit este 1, atunci avem de-a face cu un număr negativ. De exemplu, 1111 1111 în sistemul zecimal reprezintă -1. Prin urmare, 1111 0011 reprezintă -13.

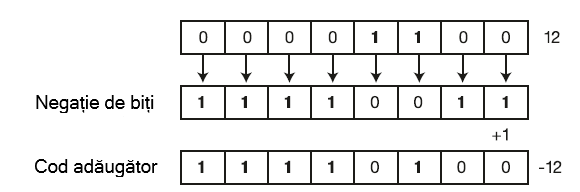
Pentru a converti un număr pozitiv într-unul negativ, este necesar să-l inversăm și să adăugăm unu.

De exemplu, să obținem numărul -3. Pentru aceasta, vom lua mai întâi reprezentarea binară a numărului 3:

310 = 0000 00112

Inversăm biții:

~0000 0011 = 1111 1100

Și adăugăm 1:

1111 1100 + 1 = 1111 1101

Astfel, numărul 1111 1101 reprezintă forma binară a numărului -3.

Să vedem cum se face adunarea între un număr semnat și unul fără semn. De exemplu, să adunăm 12 și -8:

1210 = 000011002 + -810 = 111110002 (8 - 00001000, după inversare - 11110111, după +1 = 11111000) = 410 = 000001002

Vedem că în sistemul binar am obținut numărul 000001002, echivalent cu 410 în sistemul zecimal.

Putem observa acest lucru în practică:

let num = 0b1100;     // 12 in sistemul zecimal
num = ~num;         // inversarea bitilor
num = num + 1;
console.log(num);   // -12

Operații de deplasare

Fiecare număr întreg în memorie este reprezentat sub formă de un anumit număr de biți. Și operațiile de deplasare permit deplasarea reprezentării în biți a unui număr cu un anumit număr de poziții, fie spre dreapta, fie spre stânga. Operațiile de deplasare se aplică doar operanzilor întregi. Există două operații:

• << (deplasare la stânga)

Deplasează reprezentarea în biți a numărului, reprezentată de primul operand, la stânga cu un anumit număr de poziții, specificat de al doilea operand.

const res = 2 << 2;           // 10 deplasat la stânga cu două poziții = 1000 - 8
console.log(res);      // 8

Numărul 2 în reprezentarea sa binară este 00102. Dacă sărim numărul 0010 cu două poziții la stânga, obținem 1000, care în sistemul zecimal este echivalent cu numărul 8.

• >> (deplasare aritmetică la dreapta)

Deplasează reprezentarea în biți a unui număr spre dreapta cu un număr specificat de poziții.

const res = 16 >> 3;  // 10000 deplasat la dreapta cu trei poziții = 10 sau 2 în sistemul zecimal
console.log(res);           // 2

Numărul 16 în reprezentarea sa binară este 100002. Dacă sărim numărul 10000 cu trei poziții la dreapta (ultimele trei poziții sunt eliminate), obținem 00010, care în sistemul zecimal reprezintă numărul 2.

Trebuie de menționat că aceasta este o așa-numita deplasare aritmetică, în care biții deplasați la stânga sunt umpluți cu bitul semnificativ - 0 pentru numere pozitive și 1 pentru numere negative. Astfel, la deplasarea numerelor negative nu există riscul ca acestea să devină pozitive. De exemplu:

const res = -16 >> 3;  // 11111110000 deplasat la dreapta cu trei poziții = 1111111111111110
console.log(res);      // -2

La deplasarea în dreapta a numărului -16 cu 3 poziții obținem -2, ceea ce este destul de natural.

• >>> (deplasare logică la dreapta)

Deplasează reprezentarea în biți a unui număr spre dreapta cu un număr specificat de poziții, dar, spre deosebire de operația >>, umple biții deplasați la stânga cu zerouri, adică obținem o deplasare fără semn. Astfel, chiar dacă deplasăm un număr negativ, vom obține oricum un rezultat pozitiv:

const res = -16 >>> 3;
console.log(res);      // 536870910

Se poate observa că deplasarea cu un bit la stânga este echivalentă cu înmulțirea cu 2, în timp ce deplasarea cu un bit la dreapta este echivalentă cu împărțirea la 2. Putem generaliza acest lucru: deplasarea la stânga cu n poziții este echivalentă cu înmulțirea numărului cu 2^n, în timp ce deplasarea la dreapta cu n poziții este echivalentă cu împărțirea numărului la 2^n. Aceasta poate fi folosită în locul înmulțirii/împărțirii cu puteri ale lui 2:

const res1 = 8 << 2;  // echivalent cu 8 * 4
console.log(res1);      // 32

const res2 = 64 >> 4;  // echivalent cu 64 / 16
console.log(res2);      // 4

Operațiile

Operațiile pe biți sunt efectuate numai asupra biților corespunzători ai numerelor:

• &: conjuncție pe biți (operația ȘI sau înmulțirea pe biți). Returnează 1 dacă ambii biți corespunzători ai ambelor numere sunt egali cu 1.
• |: disjuncție pe biți (operația SAU sau adunarea pe biți). Returnează 1 dacă cel puțin unul dintre biții corespunzători ai ambelor numere este egal cu 1.
• ^: XOR pe biți. Returnează 1 dacă doar unul dintre biții corespunzători ai ambelor numere este egal cu 1.
• ~: negarea pe biți sau inversarea. Inversează toți biții operandului. Dacă un bit este 1, devine 0, iar dacă este 0, devine 1.

Utilizarea operațiilor:

const a = 5 | 2;            // 101 | 010 = 111  - 7
const b = 6 & 2;            // 110 & 010 = 10  - 2
const c = 5 ^ 2;            // 101 ^ 010 = 111 - 7
const d = ~9;               // -10

De exemplu, expresia 5 | 2 este egală cu 7. Numărul 5 în reprezentare binară este 101, iar numărul 2 este 10 sau 010. Adunăm biții corespunzători ai ambelor numere. La adunare, dacă cel puțin un bit este 1, suma ambelor biți este 1. Prin urmare, obținem:

1 0 1 0 1 0 ------- 1 1 1

În final, obținem numărul 111, care în reprezentarea zecimală reprezintă numărul 7.

Să luăm o altă expresie, 6 & 2. Numărul 6 în reprezentare binară este 110, iar numărul 2 este 10 sau 010. Înmulțim biții corespunzători ai ambelor numere. Produsul celor doi biți este 1 dacă ambii biți sunt egali cu 1. În caz contrar, produsul este 0. Prin urmare, obținem:

1 1 0 0 1 0 ------- 0 1 0

Obținem numărul 010, care în sistemul zecimal este 2.